367楼老封
(......)
发表于 2007-5-3 09:39
只看此人
更简单的证法
我又找到了这题稍直接一些的证法:
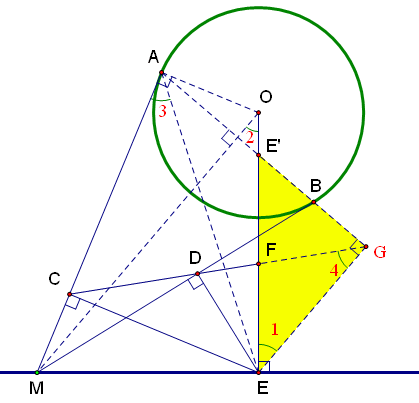
“已知定圆w,圆心为o,圆外有一定直线l,过圆心作OE垂直于l,在l上任取一动点M(不与E重合),过此点作圆的切线,切圆于A,B.现作EC垂直于MA,ED垂直于MB,连结C,D,延长交OE于F.求证F为定点。”
证明:联结OM、OA、AB、AE,并作EG⊥AB于G。
因E位于等腰三角形MAB外接圆上,故C、D、G共线(即Simson线)。
为了证明F是E′E的中点,以下只需论证GF是Rt△GE′E斜边上的中线即可。为此只需证∠1=∠4。
∵ OM⊥AB,EG⊥AB,∴OM∥EG,得∠1=∠2。
∵ O、A、M、E四点共圆,得∠2=∠3。
∵ A、C、E、G四点共圆,得∠3=∠4。
由此∠1=∠4。证毕.
附件
-
 070503.GIF
(11.04 KB)
070503.GIF
(11.04 KB)
-
2007-5-3 09:39